Elimination Puzzles¶
Process-of-elimination puzzles, sometimes known as zebra puzzles, or
just logic puzzles, are implemented in the
puzzle_solvers.elimination module. These puzzles generally
take the form of a number of different categories of items that must be
matched uniquely against each other based on rules that direct the
elimination of possibilities. An example of such a puzzle is found in
the corresponding Tutorial section.
The original “zebra puzzle” is a particular instance of this type of puzzle that originated in the December 17, 1962 issue of Life Interational. This particular formulation is ascribed to Albert Enistein, and sometimes to Lewis Carroll. A solution to this puzzle can be found among the Demos at puzzle_solvers.demos.elimination_zebra.
Contents:
Tutorial¶
As an example, we will show how to work through the problem in the Stack Overflow question that inspired this package in the first place. The full code can be found among the Demos at puzzle_solvers.demos.elimination.
The original problem statement is in German and can be found here (along with the solution). The following is as literal of a translation into proper English (US) as I could manage:
The Puzzle¶
There are five friends (Dana, Ingo, Jessica, Sören, Valerie) waiting in line at the register of a clothing store. They are all of different ages (26, 27, 30, 33, 35), and want to buy different tops (Blouse, Poloshirt, Pullover, Sweatshirt, T-Shirt) for themselves. The tops have different colors (blue, yellow, green, red, black) and sizes (XS, S, M, L, XL).
Rules¶
The top Dana wants to buy is size XL.
- She is ahead (but not directly ahead) of someone who wants to buy a black top.
Jessica waits directly in front of a person who wants to buy a Poloshirt.
The second person in line wants to buy a yellow top.
The T-shirt isn’t red.
Sören wants to buy a Sweatshirt.
- The person who waits directly in front of him is older than the one behind him.
Ingo needs a size L top.
The last person in line is 30 years old.
The oldest person is going to buy the top with the smallest size.
The person who waits directly behind Valerie wants to buy a red top.
- The red top is bigger than size S.
The youngest person wants to buy a yellow top.
Jessica is going to buy a Blouse.
The third person in line wants to buy a size M top.
The Poloshirt is either red or yellow or green.
Solution¶
Setup¶
First we import a Solver from the
puzzle_solvers.elimination module:
from puzzle_solvers.elimination import Solver
To use the Solver class, we first provide the problem space as an
input. In this case, we use a dictionary of lists. The keys of the dictionary
are the names of the categories ('top', 'age', etc.). The values are
the items in each category:
positions = [1, 2, 3, 4, 5]
names = ['Dana', 'Ingo', 'Jessica', 'Sören', 'Valerie']
ages = [26, 27, 30, 33, 35]
tops = ['Blouse', 'Poloshirt', 'Pullover', 'Sweatshirt', 'T-Shirt']
colors = ['blue', 'yellow', 'green', 'red', 'black']
sizes = ['XS', 'S', 'M', 'L', 'XL']
problem = {
'position': positions,
'name': names,
'age': ages,
'top': tops,
'color': colors,
'size': sizes,
}
The lists of values must be distinct within themselves, but not necessarily between each other. None is forbidden as either a category or item label.
All the lists are sorted as much as makes sense. This is not required by the
solver, but is convenient for us. It allows us to write something like “the
second oldest person” as ages[-2] instead of having to call a function or
hard-code 33.
Notice also that the numerical data, positions and ages is represented
as int rather than str. This allows meaningful
comparisons to be made when we get a rule that says something like “younger
than” or “standing behind”.
Then we create the solver:
solver = Solver(problem)
Internally, the solver transforms the data into a graph represented as an
adjacency matrix that keeps track of the labels and categories for you. It also
provides some methods for implementing the rules. If you want to see a detailed
report of all the operations the solver performs, pass debug=True to the
constructor.
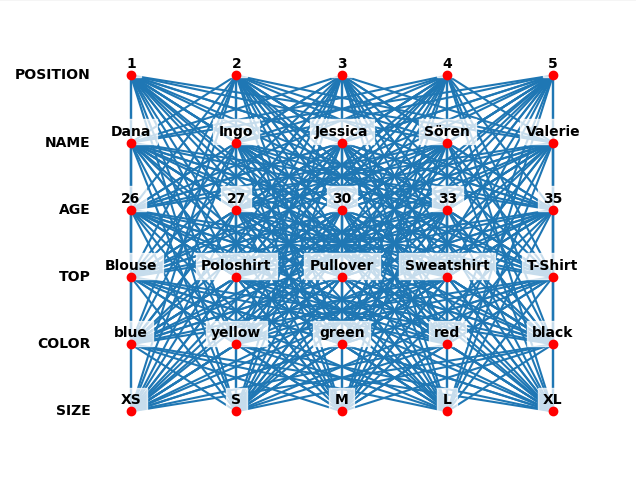
We can get a visual output of the state of the solver if matplotlib is
installed using the draw method. A quick check shows that
all the categories and items were added and linked correctly (see
(1)). Notice that there are no links within a category:
>>> solver.edges
375
>>> solver.draw()
Rules¶
The rules are added to the solver by calling the appropriate methods:
solver.match('Dana', 'XL')
The match method sets up a 1-to-1 relationship between the
name 'Dana' and the size 'XL'. As long as the names are unambiguous,
just a label is sufficient. This is a process-of-elimination problem, so the
solver removes all the possibilities that 'Dana' may be any other size, and
that anyone else might be size 'XL'. It then follows through with any
additional implications the changes
might have.
If the same label is repeated in more than one category, the category is mandatory. Items can be specified unambiguously as two-element (category, label) tuple. The line above could be rewritten as:
solver.match(('name', 'Dana'), ('size', 'XL'))
Note that all categories and labels must be an exact match with ==. As a
consequence, strings are case sensitive.
The first rule was Explicit. The next two rules are Implicit:
solver.less_than('Dana', 'black', 'position', 2, None)
solver.less_than('Jessica', 'Poloshirt', 'position', 1)
These showcase the less_than method, which creates an
Assertion that will keep getting updated as more information is
discovered about the positions of 'Dana', 'black', 'Jessica'
and 'Poloshirt'. The first call asserts that 'Dana' is at least two
positions ahead of 'black' in line. The upper bound is None. The second
call asserts that 'Jessica' is exactly one position ahead of
'Poloshirt'. There is a reflected greater_than method,
as well as an adjacent_to method that checks similar
conditions regardless of the direction.
solver.match(2, 'yellow')
solver.unmatch('T-Shirt', 'red')
unmatch eliminates a single connection. Like
match, it is Explicit. It updates
the solution with all of the resulting
implications.
solver.match('Sören', 'Sweatshirt')
solver.match('Ingo', 'L')
solver.match(positions[-1], 30)
solver.match(ages[-1], sizes[0])
solver.less_than('Valerie', 'red', 'position', 1)
solver.match('red', *sizes[sizes.index('S') + 1:])
Here, we used the fact that our positions, ages and sizes lists are
sorted. The 1-to-many form of match behaves much like the
usual form, except that the first argument can match any of the remaining
ones.
solver.match(ages[0], 'yellow')
solver.match('Jessica', 'Blouse')
solver.match(3, 'M')
solver.match('Poloshirt', 'red', 'yellow', 'green')
The categories of all the items passed to match except the
first must be the same. At this point, 116 (out of 300 (3))
edges have been eliminated:
>>> solver.edges
259
Special Cases¶
Only rule 5a has not been used up to this point. The assertions set up in steps 1a, 2 and 9 still remain, awaiting the additional infomation:
>>> solver.assertion_count
3
Looking at solver.assertions will tell us which rules are still not fully
satisfied. You will see six mappings rather than 3, because each
Assertion object is mapped twice. Assertions will remove themselves
from the assertions dictionary as they are satisfied.
Before we continue, let us pre-process the information about 'Sören' a
little bit based on the remaining rule. These steps are mainly due to a failing
of the solver, which can’t currently handle multi-level implicit rules like
that. First, we can glean that 'Sören' can not be first or last, because he
has people before and behind him:
solver.unmatch('Sören', positions[0])
solver.unmatch('Sören', positions[-1])
This still does not establish 'Sören'’s position. We can check using
category_for:
>>> solver.category_for('Sören', 'position')
This method will return a non-None value only if there is a 1-to-1 mapping
between 'Sören' in the category 'position'.
Next, we can ensure that 'Sören' is not behind the youngest person, since
the person ahead of him must be older than the one behind:
youngest = solver.category_for(ages[0], 'position')
if youngest is not None:
solver.unmatch('Sören', youngest + 1)
Here, we use category_for to find the position of the
youngest person, and unlink the preceding one from 'Sören' if it has been
established. Similarly, 'Sören' can not be directly in front of the oldest
person:
oldest = solver.category_for(ages[-1], 'position')
if oldest is not None:
solver.unmatch('Sören', oldest - 1)
This leaves us with only 10 more edges to go:
>>> solver.edges
85
The important thing is that 'Sören'’s position has been fixed, along with
everyone else’s:
>>> solver.category_for('Sören', 'position')
2
>>> solver.assertion_count
0
We can also check there are two remaining age options and two remaining
positions, both around 'Sören':
>>> solver.find_missing('position')
{1, 3}
>>> solver.find_missing('age')
{27, 33}
This is just a check. find_missing returns all the items in
category 'position' that do not have all their 1-to-1 mappings. Here is how
we code the final step:
pos = solver.category_for('Sören', 'position')
ages = solver.find_missing('age')
solver.match(pos - 1, max(ages))
solver.match(pos + 1, min(ages))
Logic¶
Structure¶
The data is presented as 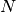 items in each of
items in each of 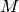 categories. We
can treat it as a graph with
categories. We
can treat it as a graph with 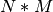 nodes. Initially, all nodes are
connected except those within a given category, for a total of
nodes. Initially, all nodes are
connected except those within a given category, for a total of
(1)¶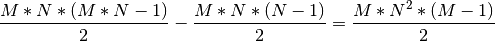
The first term on the left is the number of edges in the complete graph. The
second term on the left is the number of edges between nodes within each of the
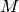 categories.
categories.
The goal of the problem is to remove edges based on provided information until
the graph ends up with 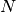 connected components, each of which is a
complete subgraph linking exactly one item from each category. The total number
of edges in the final solution is
connected components, each of which is a
complete subgraph linking exactly one item from each category. The total number
of edges in the final solution is
(2)¶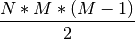
The number of edges that the information must account for is therefore
(3)¶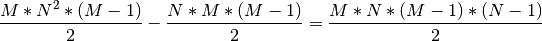
Operations¶
This solver is a process of elimination one. Naturally, the fundamental operation it currently recognizes is severing an edge. Operations are preformed in response to rules.
Rules¶
There are two types of supported rules: explicit and implicit.
Explicit¶
Explicit rules are ones that can be completely satisfied at once, and whose consequences become an integral part of the state as soon as the relevant operations are carried out. An example of a direct rule is “Red is 5”. All the necessary links can be severed immediately. Any further operations can fully take this rule into account based solely on the state it leaves behind.
Another way to look at it is that explicit rules set a direct node-to-node relationship. Because of that, explicit rules make immediate changes to the state. Any further rules must use that state to follow through with their Implications.
Implicit¶
Implicit rules are ones that can not be satisfied without additional information in the general case. That is not to say that the solver may not be in a state that allows such a rule to be satisfied immediately when it is encountered. An example of an implicit rule is “The position of Red is less than the position of 5”. Until the links between Red and 5 and the position category are fully specified through other rules, this rule can provide some information, but can not be completely represented in the state.
Implicit rules set up a relationship between nodes through a category. While
this allows for some direct changes, like unlinking the two nodes in
question, implicit rules must be revisited once more information becomes
available. Implicit rules are stored in Assertion objects and
re-evaluated whenever any potential endpoints change.
Implications¶
The most important aspect of this solver is its ability to follow through with
the implications of an edge removal. To illustrate exactly what this means,
let’s say we have categories 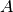 and
and 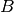 with an item
with an item 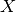 in
in
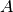 and
and 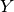 in
in 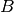 . When edge
. When edge 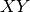 is severed, it
affects the relationship between
is severed, it
affects the relationship between 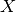 and
and 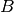 . The nodes in
. The nodes in
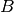 that
that 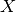 is still connected to determine the entire set of
connections that are allowed for
is still connected to determine the entire set of
connections that are allowed for 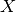 elsewhere. Any connections that
elsewhere. Any connections that
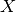 has to nodes not also connected to the nodes it is connected to in
has to nodes not also connected to the nodes it is connected to in
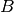 must be severed. The process is recursive. It applies to
must be severed. The process is recursive. It applies to 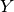 and
and 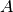 by symmetry.
by symmetry.
Single-edge removal is implemented in the Solver.unmatch method.
A 1-to-many match between two categories is equivalent to removing multiple
edges. Mapping node 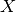 in category
in category 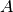 to a number of
possibilities in category
to a number of
possibilities in category 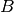 is equivalent to severing all the edges to
nodes in
is equivalent to severing all the edges to
nodes in 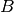 that
that 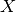 does not map to. A slight optimization is
possible by processing the severance from
does not map to. A slight optimization is
possible by processing the severance from 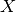 as a single unit.
as a single unit.
An even more specialized application is creating a 1-to-1 match this is the symmetrical extension of a 1-to-many match. All the nodes connected to one matched node must share an edge with the other as well. Any edges not meeting this criterion must be severed.
Matching to a single element of one category, both 1-to-1 and 1-to-many, is
implemented in the Solver.match method.
The final aspect of implications is that all affected categories must be
checked against the implicit rules encountered up to that point. In the
examples above, all the indirect rules linked through either 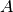 or
or
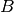 would have to be re-verified. Any edge removal affects the indirect
rules at both ends, since the contents of the categories changes.
would have to be re-verified. Any edge removal affects the indirect
rules at both ends, since the contents of the categories changes.
API¶
The API for elimination puzzles revolves around the user-facing
Solver class.
-
class
puzzle_solvers.elimination.Solver(problem, categories=None, debug=False)¶ The solver class represents an elimination problem as an adjacency matrix of size
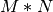 , where
, where 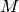 is the number of
categories and
is the number of
categories and 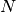 is the number of elements. The matrix is
symmetrical, with size-
is the number of elements. The matrix is
symmetrical, with size-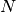 identity matrices all along the
diagonal.
identity matrices all along the
diagonal.The class provides two types of operations: high level and low level. High level operations accept item labels or (category, item) tuples as inputs. They make it easy to implement the elimination rules of the puzzle. Low level methods accept matrix coordinates in the range
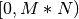 .
. matchandunmatchare examples of high-level methods. Low-level methods support the logic of high level methods.unlinkandfind_matchesare low level methods.Positions used by the low level methods can be converted to an index within
categoriesand an index within that category usingdivmod: the quotient withnis the category index, while the remainder is the index within the category.-
__init__(problem, categories=None, debug=False)¶ Create a solver for a particular incarnation of the zebta puzzle.
The problem can be specified as either a mapping of category labels to iterables of items or an iterable of iterables. In the latter case, the category labels can be the first element of each iterable, or supplied independently. In either case, all labels may be of any hashable type. All item iterables must contain the same number of elements. The labels for each item must be unique within a category, but may be repeated between categories. So a
'Height'of72and an'Age'of72are possible in the same problem, but two items can’t both have a'Height'of72. Category labels must be unique as well, but a category and any item can have the same label.Completely unique item labels can be supplied to the high level methods as just the item label (unless the label itself is a tuple). Item labels that are repeated between categories must always be supplied as a two-element (category, item) tuple.
No item or category labels may be None.
Parameters: - problem – The problem is specified as either a mapping of iterables, or an iterable of iterables.
- categories – If problem is a mapping, this parameter is ignored.
Otherwise, if supplied, the iterables in problem are
interpreted as having
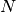 elements, while this
iterable supplies the
elements, while this
iterable supplies the 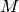 category labels. If missing,
and first element of each iterable in problem is the
category label. Must be the same length as problem if
used.
category labels. If missing,
and first element of each iterable in problem is the
category label. Must be the same length as problem if
used. - debug (bool) – A flag indicating whether or not detailed messages should be printed by all the methods.
-
adjacent_to(item1, item2, category, *bounds)¶ -
adjacent_to(item1, item2, category[, exact=1])
-
adjacent_to(item1, item2, category[, lower, upper])
Assert that the item in category linked to item1 is within some bounds on either side of the one linked to item2.
The items may or may not be in the same category, but at least one of their categories must differ from category. All the item labels in category must be comparable in a way that makes sense, which usually means that they are numbers.
item1 and item2 may be either a label or a two-element (category, label) tuple. The latter is required if a label is ambiguous is a tuple. The category will be determined automatically in the former case.
First, item1 and item2 will be
unmatched. After that, any possibilities that contradict the assertion at the time of invocation are removed. If the assertion is not fully satisfied, a listener in the shape of anAssertionis set up to continue monitoring for additional link removals. TheAssertionremoves itself as soon as it is satisfied.The exact type of assertion depends on the bounds that are specified:
- No bounds :
AdjacencyOffsetAssertion- Single, exact bound :
AdjacencyOffsetAssertion- Two Bounds, upper and lower :
BoundedAssertion
Parameters: - item1 – The lesser item to compare.
- item2 – The greater item to compare.
- category – The category in which to make the comparison.
- bounds – Optional bounds for the difference being asserted. If one bound is provided, it is an exact match: item1 is exactly *bounds less than item2. If two bounds are provided, they are the inclusive limits for the difference. A bound of None indicates unbounded (only allowed for the upper bound).
Returns: count – The total number of links removed. Zero if the items already satisfy the assertion. Any further removals are made in response to additional explicit rules being added to the solver.
Return type: Notes
If bounds are specified, either as an exact match or a range, the labels in category must support subtraction (
-operator) as well as the<operator in a meaningful manner. Normally, this method will be used for numbers, so the restriction is fairly straightforward.-
-
assertion_count¶ The number of active
assertions.
-
assertions¶ A mapping of (position, category IDs) pairs to
Assertions.This mapping is mutable. It is checked whenever an edge is removed. Assertions should be added via methods like
greater_thanandadjacent_to. Removal should be automatic when they aresatisfied, via theremove_assertionmethod.Each assertion object appears under two keys in the mapping: one for each of the items that it links together. Assertions are stored in a list under each key.
-
available_for(item, category)¶ Find all the items in category that item can still link to.
item may be either a label or a two-element (category, label) tuple. The latter is required if the label is ambiguous or a tuple. The category will be determined automatically in the former case.
Parameters: - item – The item to search for links with.
- category – The category to search in.
Returns: labels – The item labels in category that item can still link to.
Return type:
-
cat_mask(cat)¶ Create a mask that is ones in the block of
nelements corresponding to cat, and False elsewhere.
-
categories¶ The labels of the categories in this problem.
This is a tuple of length
m, containing unique elements.
-
category_for(item, category)¶ Determine if item has a 1-to-1 mapping to category.
1-to-1 mappings can be set up with
match, or occur naturally as a consequence of other link removals.item may be either a label or a two-element (category, label) tuple. The latter is required if item is ambiguous or the label is a tuple. The category will be determined automatically in the former case.
Parameters: - item – The item to search for links with.
- category – The category to search in.
Returns: - If a mapping is found, return it as an item label. Otherwise,
- return None.
-
draw(show=True, title=None)¶ Draw the adjecency matrix as a diagram using matplotlib.
Each category is displayed in its own row. Items within the category appear in the order they were passed in to the constructor in.
Edges representing 1-to-1 mapping between categories are highlighted. A solved problem will contain only highlighted edges.
This method is disabled (raises a
NotImplementedErrorif matplotlib is not found),Parameters: - show (bool) – Whether or not to show the figure after drawing it. Default is True.
- title – An optional title to assign to the figure.
Returns: - fig – The figure that the diagram was drawn on.
- ax – The axes that the diagram was drawn on.
-
edges¶ The total number of edges remaining in the solution.
-
find_matches(pos)¶ Find all items with single links across categories to pos.
A matching item is one that is the only one in its category that shares an edge with the item at pos.
Parameters: pos (int) – A row or column in matrix.Returns: matches – A numpy array containing the matching positions. Return type: numpy.ndarray
-
find_missing(category)¶ Retrieve a set of all the items in category that do not have all of their 1-to-1 mappings set.
Parameters: category – The category to search in. Returns: missing – A set of item labels in category that still require work. Return type: set
-
greater_than(item1, item2, category, *bounds)¶ -
greater_than(item1, item2, category[, exact])
-
greater_than(item1, item2, category[, lower, upper])
Assert that the item in category linked to item1 is greater than the one linked to item2.
The items may or may not be in the same category, but at least one of their categories must differ from category. All the item labels in category must be comparable in a way that makes sense, which usually means that they are numbers.
item1 and item2 may be either a label or a two-element (category, label) tuple. The latter is required if a label is ambiguous is a tuple. The category will be determined automatically in the former case.
First, item1 and item2 will be
unmatched. After that, any possibilities that contradict the assertion at the time of invocation are removed. If the assertion is not fully satisfied, a listener in the shape of anAssertionis set up to continue monitoring for additional link removals. TheAssertionremoves itself as soon as it is satisfied.The exact type of assertion depends on the bounds that are specified:
- No bounds :
BoundedExclusiveAssertion- Single, exact bound :
OffsetAssertion- Two Bounds, upper and lower :
BoundedAssertion
Parameters: - item1 – The greater item to compare.
- item2 – The lesser item to compare.
- category – The category in which to make the comparison.
- bounds – Optional bounds for the difference being asserted. If one bound is provided, it is an exact match: item1 is exactly *bounds less than item2. If two bounds are provided, they are the inclusive limits for the difference. A bound of None indicates unbounded (only allowed for the upper bound).
Returns: count – The total number of links removed. Zero if the items already satisfy the assertion. Any further removals are made in response to additional explicit rules being added to the solver.
Return type: Notes
If bounds are specified, either as an exact match or a range, the labels in category must support subtraction (
-operator) as well as the<operator in a meaningful manner. Normally, this method will be used for numbers, so the restriction is fairly straightforward.This method is a convenience wrapper for
solver.less_than(item2, item1, category, *bounds)
This is generally not a problem, unless you happen to have labels in category whose comparison operations do not reflect properly.
-
-
item_to_pos(item)¶ Convert a two-element (category, value) item tuple into a matrix position and category index.
Parameters: item – Either a two-element (category, label) tuple, or just an item label. Item labels are only accepted if they are not tuples and are unambiguous across the entire problem space. Returns: - pos (int) – The index of the item within the
matrix. - cat (int) – The index of the item’s category within
categories.
- pos (int) – The index of the item within the
-
labels¶ The data labels corresponding to each row/column of
matrix.This is a tuple of
m*nelements, not all of which are guaranteed to be unique. Theelements in each successive subsequence ofnare unique though.
-
less_than(item1, item2, category, *bounds)¶ -
less_than(item1, item2, category[, exact])
-
less_than(item1, item2, category[, lower, upper])
Assert that the item in category linked to item1 is less than the one linked to item2.
The items may or may not be in the same category, but at least one of their categories must differ from category. All the item labels in category must be comparable in a way that makes sense, which usually means that they are numbers.
item1 and item2 may be either a label or a two-element (category, label) tuple. The latter is required if a label is ambiguous is a tuple. The category will be determined automatically in the former case.
First, item1 and item2 will be
unmatched. After that, any possibilities that contradict the assertion at the time of invocation are removed. If the assertion is not fully satisfied, a listener in the shape of anAssertionis set up to continue monitoring for additional link removals. TheAssertionremoves itself as soon as it is satisfied.The exact type of assertion depends on the bounds that are specified:
- No bounds :
BoundedExclusiveAssertion- Single, exact bound :
OffsetAssertion- Two Bounds, upper and lower :
BoundedAssertion
Parameters: - item1 – The lesser item to compare.
- item2 – The greater item to compare.
- category – The category in which to make the comparison.
- bounds – Optional bounds for the difference being asserted. If one bound is provided, it is an exact match: item1 is exactly *bounds less than item2. If two bounds are provided, they are the inclusive limits for the difference. A bound of None indicates unbounded (only allowed for the upper bound).
Returns: count – The total number of links removed. Zero if the items already satisfy the assertion. Any further removals are made in response to additional explicit rules being added to the solver.
Return type: Notes
If bounds are specified, either as an exact match or a range, the labels in category must support subtraction (
-operator) as well as the<operator in a meaningful manner. Normally, this method will be used for numbers, so the restriction is fairly straightforward.-
-
linked_set(pos, cat)¶ Find all links between the specified position and category.
Parameters: - pos (int) – The index of an item within the
matrix. - cat (int) – The index of a category within
categories.
Returns: links – All items in cat linked to pos, as indices within
matrix.Return type: - pos (int) – The index of an item within the
-
m¶ The number of categories in this problem (read-only).
-
map¶ A mapping of the unambiguous item labels to their index in
matrix.Ambiguous labels are mapped to None. This mapping is read-only.
-
match(item1, item2, *items)¶ Associate item1 exclusively with item2 and possibly some other items in the same category as item2.
A 1-to-1 mapping is one that sets up an equivalence, for example “the person in the Green shirt is 72” tall”. 72” can connect only to Green in the Color category, and Green can connect only to 72” in the height category. Their other connections must be shared as well. This method recursively applies the logical implications of that pruning.
A 1-to-many mapping is a partial equivalence, like “the person in the Green shirt can be 70”, 72”, or 75” tall”. Green can connect only to those three items in the Height category, but they can (and two of them must) connect to other items in the Color category. All connections to other categories that Green has must be present in at least one of the Height items as well. This method recursively applies the logical implications of that pruning as well.
The inputs may be either item labels or two-element (category, label) tuples. The latter is required if items are ambiguous or the labels are tuples. The category will be determined automatically in the former case.
The category of item1 and item2 may not be the same unless they are the same item. Any additional items must have the same category as item2.
This method removes all possible links from item1 to items in the the category of item2 that are not in the set comprised of item2 and items. See the Logic section for more information.
Parameters: - item1 – A single item to match.
- item2 – Either a single item or one item of a number from the same category to match.
- items – Optional additional items from the same category as item2.
Returns: count – The total number of links removed. Zero if the items already satisfy the match.
Return type:
-
matrix¶ The current state of the solver represented as a square numpy array with
m*nelements to a side. The array is a boolean, symmetric adjacency matrix with True all along the main diagonal.
-
n¶ The number of items in this problem (read-only).
-
pos_mask(pos)¶ Create a mask that only has the bit at pos set to True.
-
pos_to_item(pos, cat=None)¶ Convert a matrix position to a (category, label) tuple.
Parameters: - pos (int) – The index of the item in
matrix. - cat (int) – An optional index of the category in
categories. If omitted, it is computed aspos // n.
Returns: item – A two-element (category, label) tuple providing an unambiguous high-level reference to the item.
Return type: - pos (int) – The index of the item in
-
register_assertion(assertion)¶ Add assertion to
assertionsso that it can be triggered as part of implication analysis.This is a utility method that should not be called by the user directly under normal circumstances. It is used by the methods that implement Implicit rules.
-
remove_assertion(assertion)¶ Remove assertion from
assertionsso that it will no longer be triggered in implication analysis.This is a utility method that should not be called by the user directly under normal circumstances. It is used by
Assertion.updatewhen the assertion issatisfied.
-
reset()¶ Resets the solver to its initial state.
This method regenerates the adjacency matrix and removes all assertions.
-
solved¶ Indicates whether the number of remaining edges matches what it would have to be for a complete solution.
-
unlink(pos1, pos2)¶ Set two items to be definitely not associated.
All edges between items associated with either one are updated as well.
This is the low-level equivalent of
unmatch: the inputs are matrix positions.Unlinking already unlinked items is a no-op. Unlinking an item from itself is an error. The updated relationships are pruned recursively according to the description in the he Logic section.
Parameters: - pos1 – The matrix position of an item to unmatch.
- pos2 – The matrix position of the item to unmatch it from.
Returns: count – The number of edges removed. Zero if the items are already unlinked.
Return type:
-
unmatch(item1, item2)¶ Set two items to be definitely not associated.
All links between items associated with either one are updated as well.
The inputs may be either item labels or two-element (category, label) tuples. The latter is required if items are ambiguous or the labels are tuples. The category will be determined automatically in the former case.
Unmatching already unmatched items is a no-op. Unmatching an item from itself is an error. The updated relationships are pruned recursively according to the description in the he Logic section.
Parameters: - item1 – An item to unmatch.
- item2 – The item to unmatch it from.
Returns: count – The number of edges removed. Zero if the items are already unmatched.
Return type:
-
-
class
puzzle_solvers.elimination.Assertion(solver, item1, item2, category, key=None)¶ Implements indirect rules for the solver.
Assertions do not exist independently of a
Solver. They are registered through high-level methods likeSolver.greater_than, and removed once they aresatisfied.An example of an assertion is “The green thing is next to the 78lb thing”. Until the implicit position of both “green” and “78lb” are known, the assertion will hang around and hopefully help prune some edges here and there.
In general, assertions link two nodes through a category. The category may be the category of either linked item, but usually is not in practice.
This class is abstract. Child classes are provided to implement the various comparisons supported by the solver. The list of assertions currently provided by the module is based on the instances of puzzles that inspired it rather than completeness. Feel free to add more, and give examples of the sorts of rules they implement.
-
__init__(solver, item1, item2, category, key=None)¶ Set up an assertion linking two items of interest via a category.
item1 and item2 may be either a label or a two-element (category, label) tuple. The latter is required if a label is ambiguous is a tuple. The category will be determined automatically in the former case.
Depending on the assertion, the order of the items may matter.
Parameters: - solver (Solver) – The solver that this assertion operates in.
- item1 – The first item of interest.
- item2 – The second item of interest.
- category – The label of the category that links the items.
-
__repr__()¶ Return a computer-readable-ish string representation.
-
__str__()¶ Return a human readable string representation.
The default implementation delegates to
__repr__, so child classes should override it.
-
cat¶ The index of the category through which the items in this assertion are linked.
This may or may not be the same as either of
cat1andcat2, but it can’t be the same as both.
-
cat1¶ The category index of the first item this assertion links, as an index into
solver’scategories.
-
cat2¶ The category index of the second item this assertion links, as an index into
solver’scategories.
-
default_key(solver, pos)¶ The default value for comparison is just the solver’s label at pos.
The key function can either be passed in the constructor or overriden in a child class. In either case, it must accept a
Solverobject and a matrix position as arguments.
-
is_valid(key, options, reverse=False)¶ Verify that there is at least one option
optin options that returns True forop(key, opt).The key is just the item label by default, but does not have to be.
The default implementation performs a linear search of options using
op. This method is provided to allow children to optimize the comparison.Parameters: Returns: The first encountered option that makes item valid, or None if invalid.
Return type: opt
-
key¶ A function that maps the items in
catto comparable values.This function must accept a
Solverand a matrix position as arguments. The return value is the type of key thatopsupports. The default implementation of this method isdefault_key, which just maps the position to the corresponding label.All currently implemented assertions have a built-in assumption that the result of this function will be a number, but this is not a requirement in the general case.
-
op(key1, key2)¶ The comparison operation that this assertion represents.
This method is applied to items in the linking category after the key function has been applied to them. The key function is just the item label by default, but does not have to be. The order of the inputs matters (in the general case).
Parameters: - key1 – The first (left) item key to compare.
- key2 – The second (right) item key to compare.
Returns: A flag determining if the comparison succeeded or not.
Return type:
-
satisfied¶ Determines if this assertion has been satisfied based on the additional information provided to the solver.
An assertion is satisfied when the number of links between each of the items of interest and the linking category is one.
-
update(pos12, posC)¶ Called when a link that is between either
pos1orpos2and posC incatis severed.The default is to re-
verifythe assersion as long as pos12 is indeed eitherpos1orpos2and posC is incat.An assertion must remove itself if it is satisfied by an update.
-
verify()¶ Check the assertion for all available links from the items to the category, and remove any invalid possibilities.
This method may end up being recursive if a link removal triggers a re-verification of this assertion. In that case, the current execution will be aborted in favor of the updated one.
-
-
class
puzzle_solvers.elimination.OffsetAssertion(solver, item1, item2, category, offset)¶ Assert that two items are a fixed distance from each other in a particular order.
-
__init__(solver, item1, item2, category, offset)¶ Set up an assertion that
item2 - item1 == offset.Parameters: - solver (Solver) – The solver that this assertion operates in.
- item1 – The first item of interest.
- item2 – The second item of interest.
- category – The label of the category that links the items.
- offset – The required difference between the items, with sign and magnitude.
-
__repr__()¶ Return a computer-readable-ish string representation.
-
__str__()¶ Return a human readable string representation.
-
is_valid(key, options, reverse=False)¶ An optimized version of the default
Assertion.is_validmethod.Since
offsetis fixed, a simple check as to whetherkey + offsetis in options suffices. For the reverse case, we checkkey - offset.
-
offset¶ The offset separating the items.
-
op(key1, key2)¶ Checks if the difference between two items is
offset.The difference is computed by
AsymmetricAssertionMixin.value.
-
-
class
puzzle_solvers.elimination.AdjacencyOffsetAssertion(solver, item1, item2, category, offset)¶ Assert that two items are a fixed distance from each other, regardless of direction.
-
__str__()¶ Return a human readable string representation.
-
is_valid(key, options, reverse=False)¶ An optimized version of the default
Assertion.is_validmethod.Since
offsetis fixed, a simple check as to whether one ofkey + offsetorkey - offsetis in options suffices.
-
-
class
puzzle_solvers.elimination.BoundedAssertion(solver, item1, item2, category, lower, upper)¶ Assert that two items are withn a range of values from each other, like
BoundedExclusiveAssertion, but inclusive of both ends.The direction matters for this assertion.
-
__init__(solver, item1, item2, category, lower, upper)¶ Set up an assertion that
[lower <=] item2 - item1 [<= upper].Parameters: - solver (Solver) – The solver that this assertion operates in.
- item1 – The first item of interest.
- item2 – The second item of interest.
- category – The label of the category that links the items.
- lower – The optional lower bound for the comparison. If omitted the difference just has to be less than or equal to upper.
- upper – The optional upper bound for the comparison. If omitted the difference just has to be greater than or equal to lower.
-
__repr__()¶ Return a computer-readable-ish string representation.
-
__str__()¶ Return a human readable string representation.
-
bounds(reverse)¶ Compute the bounds of the space of possibilities for the difference between the items.
This method should only be used after checking that
loweranduppercan both be negated. It allows child classes to override the type of difference the assertion checks for.If reverse is set, the bounds are reversed and negated.
-
is_valid(key, options, reverse=False)¶ In some cases, it is possible to optimize the default
Assertion.is_validmethod.If both bounds are
int, meaning that the search space is finite and discrete, it may be faster to check the range of offsets rather than finding a match in options directly. The reverse case is computed by swapping the bounds and their signs.If an optimization is possible, the bounds of the search space are is computed by
bounds, the iterator over the space byspace, and the size of it bynspace.
-
lower¶ The inclusive lower bound of the comparison.
If None, the comparison is unbounded on the low end.
-
nspace()¶ The number of elements in the iterator returned by
space.This method allows a check to determine if the search can be optimized before actually creating the iterator. This method should only be used after ensuring that
lowerandupperare both integers. It allows child classes to override the type of difference that the assertion checks for.
-
op(key1, key2)¶ Check if the difference between two items is between
lowerandupper, inclusive.Unset bounds are not checked. That part of the test always evaluates to True.
The difference is computed by
AsymmetricAssertionMixin.value.
-
space(key, lower, upper)¶ Create an iterator of all valid possibilities with key as the first item in the comparison.
This method should only be used after ensuring that lower and upper are both integers. It allows child classes to override the type of difference that the assertion checks for.
-
upper¶ The inclusive upper bound of the comparison.
If None, the comparison is unbounded on the high end.
-
-
class
puzzle_solvers.elimination.BoundedExclusiveAssertion(solver, item1, item2, category, lower, upper)¶ Assert that two items are withn a range of values from each other, like
BoundedAssertion, but exclusive of both ends.The direction matters for this assertion.
-
__str__()¶ Return a human readable string representation.
-
nspace()¶ The number of elements in the iterator returned by
space.This method allows a check to determine if the search can be optimized before actually creating the iterator. This method should only be used after ensuring that
lowerandupperare both integers. It allows child classes to override the type of difference that the assertion checks for.
-
op(key1, key2)¶ Check if the difference between two items is between
lowerandupper, exclusive.Unset bounds are not checked. That part of the test always evaluates to True.
The difference is computed by
AsymmetricAssertionMixin.value.
-
space(key, lower, upper)¶ Create an iterator of all valid possibilities with key as the first item in the comparison.
This method should only be used after ensuring that lower and upper are both integers. It allows child classes to override the type of difference that the assertion checks for.
-
-
class
puzzle_solvers.elimination.BandedAssertion(solver, item1, item2, category, lower, upper)¶ Assert that two items are with a range of values from eachother, irrespective of direction, inclusive of both bounds.
-
__str__()¶ Return a human readable string representation.
-
bounds(reverse)¶ Compute the bounds of the space of possibilities for the difference between the items.
This method ignores reverse because the bounds are symmetric about the origin. Both bounds should be positive.
-
nspace()¶ The number of elements in the iterator returned by
space.The value returned by this method is twice the one returned by
BoundedAssertion.nspacebecause it is symmetric about the origin.This method allows a check to determine if the search can be optimized before actually creating the iterator. This method should only be used after ensuring that
lowerandupperare both integers. It allows child classes to override the type of difference that the assertion checks for.
-
space(key, lower, upper)¶ Create an iterator of all valid possibilities with key as the first item in the comparison.
The iterator will contain two distjoined portions.
This method should only be used after ensuring that lower and upper are both integers. It allows child classes to override the type of difference that the assertion checks for.
-